www.plusplanet.de
Schulinfos von F. Töns
Schulinfos von F. Töns
21.04.2021
Abiturvorbereitung:Aufgabensammlung (mit Lösungen) aus dem Abitur 2011
www.plusplanet.de/miscrawhtml/20210400_Abiturvorbereitung_4.pdf
... und ein dazugehöriger Podcast.
www.plusplanet.de/video/20210420_podcast_abitraining_low.mp3
15.04.2021
Abiturvorbereitung:(Analysisaufgaben wie letzte Stunde)
Analysis Teil 2 Aufgabe: http://www.plusplanet.de/miscrawhtml/20210413_abivorbereitung_ana2_auf.jpg )
Analysis Teil 2 Lösung: http://www.plusplanet.de/miscrawhtml/20210413_abivorbereitung_ana2_lsg2.jpg )
(Analysisaufgaben zu Geraden und Tangenten)
Analysis Teil 3 Aufgabe: http://www.plusplanet.de/miscrawhtml/20210414_abivorbereitung_ana3_auf.jpg )
Analysis Teil 3 Lösung: http://www.plusplanet.de/miscrawhtml/20210414_abivorbereitung_ana3_lsg.jpg )
(Vektorrechnung: Geraden, Ebenen, Schnittpunkt)
Vektoren Teil 1 Aufgabe: http://www.plusplanet.de/miscrawhtml/20210414_abivorbereitung_lina1_auf.jpg )
Vektoren Teil 1 Lösung: http://www.plusplanet.de/miscrawhtml/20210414_abivorbereitung_lina1_lsg.jpg )
12.04.2021
Abiturvorbereitung:(Direktlink: http://www.plusplanet.de/miscrawhtml/20210412_abivorbereitung_ana.jpg )
(Lösung: http://www.plusplanet.de/miscrawhtml/20210412_abivorbereitung_ana_lsg.jpg )

24.03.2021
Abiturprüfungen der vergangenen Jahre
Bitte beachtet folgendes:
* Es gibt bei den schriftlichen Prüfungen jeweils eine PDF-Datei mit Aufgaben und ein dazugehöriges Lösungsdokument.
* Erklärung der Namenskonventionen: Beispiel "M_17_t_G_HT_B5_GG_A"
*** M für Mathe
*** 17 für das Jahr 2017
*** t (normale Aufgabe) oder x (Hilfsmittelfreier Teil (HFT))
*** G für Grundkurs (oder L für Leistungskurs)
*** HT für Haupttermin (es gibt ja auch Nachschreibtermine)
*** B5 Themanummer (es gibt normalerweise 5 verschiedene Aufgaben in jedem Jahr) bzw. A1 für den HFT
*** GG ... keine Ahnung
*** L für Lösung (oder A für Aufgabenstellung)
Zusätzlich zu den unten bereitgestellten Drittfach-Klausuren habe ich ein paar Materialien für die Viertfach-Prüfungen ins gleiche Verzeichnis gestellt. Da die Lösungen für die Aufgaben nur für meine Kolleginnen oder Kollegen bestimmt sind, sind sie für Euch vielleicht nicht immer nachvollziehbar. Ihr könnt mir gerne Fragen per Mail dazu stellen.
Die drei relevanten Dateien heißen:
* Abi4mdl_20120510_Abi_Fach4_mdl2_verbraten_fuer_vm.pdf
* Abi4mdl_20160300_mundliche_prufungen_test.pdf
* Abi4mdl_20160427_Vektor_ganzrat_anonymisiert_als_VM_Uebung.pdf
Außerdem müsst ihr wissen, dass der zweite Prüfungsteil ein relativ spontanes Frage-Antwort-Spielchen ist, welches man nur schlecht planen kann. Die Notizen dazu sind deswegen auf den obigen Dokumenten etwas knapp.
* Bitte gebt die Zugangsdaten NICHT an Bekannte weiter, da es ein Download-Limit auf meiner Seite gibt: Wenn mehr als ein paar Dutzend Leute auf die Daten zugreifen, wird die Webseite gesperrt.
Die Dateien finden sich in einem geschützen Verzeichnis.
Der Benutzername lautet: mathe2021
Das Kennwort lautet: Die Schul-Email-Adresse von mir.
Hier nun der Link aufs Verzeichnis:
http://www.plusplanet.de/htaccessdir/
16.06.2020
Lieber MathekursBitte beachtet folgende Aufgabe zur Binomialverteilung
www.plusplanet.de/miscrawhtml/20210224_Anwendung_Binomialverteilung.jpg
www.plusplanet.de/miscrawhtml/20210228_Anwendung_Binomialverteilung_abwandlung1_low.jpg
www.plusplanet.de/miscrawhtml/20210228_Anwendung_Binomialverteilung_abwandlung2_low.jpg
Und ein Podcast für die Abiklausur 2019, Thema 5:
www.plusplanet.de/video/20210228_podcast_abi2019_b5_gk_low.mp3
16.06.2020
Lieber MathekursWie verabredet hier noch eine Aufgabe für die letzte Schulwoche:
Auf Seite 3 des bereits beim letzten Mal verlinkten Dokumentes ( 00000000_M13_LA10_Vektoren_Einfuehrung.pdf ) gibt es drei Aufgaben.
Wir sparen uns mal Aufgabe 1. Aber Aufgabe 2 ist tatsächlich wichtig fürs Verständnis:
Beispiel: Bei Aufgabe 2a rechnet man das Ergebnis aus. Das Ergebnis ist ja zunächst ein Vektor (also die Zahlen 3 und 2 übereinandergeschrieben). In der Aufgabe steht nun, dass dieses Ergebnis als Ortsvektor aufgefasst werden soll, d.h. als einen Vektor, der vom Koordinatenursprung aus auf den Punkt P(3|2) zeigt. Es soll nun in ein Koordinatensystem nur der Punkt P eingezeichnet werden. Wenn alle sechs Teilaufgaben erledigt sind, kann man bei den gezeichneten Punkten eine Regelmäßigkeit erkennen. Welche? Und warum?
Bei Aufgabe 3 muss man ein wenig knobeln.
Bearbeitung der Aufgabe 2 und Aufgabe 3 bis zum Dienstag, den 23.06.2020
Bonusaufgabe
In der Bilderfolge unten könnt ihr sehen, wie man ein 3D-Logo bauen kann. Ich empfehle folgende Schritte:
1. Ihr habt ja im Unterricht ein Zettel bekommen, auf dem das gesamte Alphabet abgedruckt ist. Alle Buchstaben sind genau 3cm breit (also 6 Kästchen) und 5cm hoch (also 10 Kästchen). Ich habe mich nun für die Buchstaben "GBG" entschieden. Diese habe ich nochmal selbst aufs Kästchenpapier gezeichnet, um ein Gefühl für die Buchstaben zu bekommen. Fast alle Ecken liegen auf "ganzen Zentimetern", also auf den dick markierten Punkten.
2. Man macht sich im 3D-Koordinatensystem klar, in welchen "Boxen" die Buchstaben liegen sollen (siehe erstes Bild oben links). Diese Boxen sind jeweils 3x5x1 Einheit groß, so dass jeweils genau ein Buchstabe mit einer "Dicke" von 1 in diese Boxen hineinpasst.
3. Man zeichnet die Vorderseiten der Buchstaben auf die Boxen auf (Bild 2). Bitte arbeitet hier sehr genau! Insbesondere bei dem linken "G" und bei dem liegenden "B" muss man wirklich gewissenhaft zählen (sonst wirds halt nur irgendwie halbgar). Beispiel "B": Der normale Buchstabe ist ja 5cm hoch. Da das "B" aber flach liegen soll, müssen wir nun 5 Einheiten entlang der x1-Achse gehen, um die "Höhe" des "B" abzugehen. Hangelt Euch immer an den Achsen entlang!
4. Beim dritten Bild werden die Buchstaben eine Einheit "dick" gemacht.
5. Wer sich künstlerisch austoben möchte, macht noch eine Schattierung. Dabei hilft es, wenn man sich vorstellt, von wo das Licht kommen soll (bei mir ist links oben von der Abbildung meine gedachte Lichtquelle)
6. Ihr sollt immer in der Lage sein, jede Ecke mit Koordinaten bezeichnen zu können. Beispielsweise hat die ganz linke untere Ecke des "B" die Koordinaten (5|0|-1).
Aufgabe: Zeichne zwei oder drei Buchstaben in der Art, wie ich es gemacht habe. Nimm beispielsweise die ersten Buchstaben deines Vornamens und deines Nachnamens.
Über sauber gezeichnete Kunstwerke freue ich mich. Gerne kann ich diese auch auf diese Webseite setzen, wenn ihr wollt.

Für die Zocker unter Euch: 3D-Tetris:
https://www.youtube.com/watch?v=ay5tD8SbBKU
Das Programm kann kostenlos heruntergeladen werden:
http://www.blockout.net/blockout2/
Im Wikipedia-Artikel zu Blockout steht:
Der positive Einfluss auf die Raumvorstellung Jugendlicher (10- bis 14-Jähriger) konnte 1993 im Rahmen einer wissenschaftlichen Studie nachgewiesen werdenhttps://de.wikipedia.org/wiki/BlockOut
12.06.2020
Lieber MathekursWir sollten kurz vor den Sommerferien nicht abschlaffen und uns noch ein wenig mit dem Thema beschäftigen, welches eigentlich in diesen Wochen im Unterricht behandelt werden müsste: Vektorrechnung.
Anstatt hier lange Erklärungen zu schreiben, möchte ich Euch zwei Videos empfehlen:
https://www.youtube.com/watch?v=mV3ljzoofKk
https://www.youtube.com/watch?v=O-7rPZ_KXFo
Ich hoffe, dass Ihr damit eine Vorstellung davon bekommt, was ein Vektor ist und wie man damit rechnen kann.
Nun lernt man bekanntlich durch Anschauen von Mathe-Videos genausoviel Mathe wie man durch bloßes Anschauen von Fitnessvideos Muckis bekommt. Also ladet Euch bitte folgendes Dokument herunter und füllt die Lücken auf Seite 1 aus und bearbeitet Aufgabe 1 auf Seite 2. Die anderen Aufgaben können wir später machen.
00000000_M13_LA10_Vektoren_Einfuehrung.pdf
Bearbeitung der Aufgabe bis zum Dienstag, den 16.06.2020 - unser nächster Unterrichtstermin im GBG.
18.05.2020
Klausurthemen an Q1• Exponentialfunktionen
• Bedeutung der Zahl e
• Exponentialfunktionen im Sachzusammenhang, Exponentialfunktionen finden
• Ableiten von Funktionen mit Produkt- und Kettenregel
• Kurvenuntersuchung von zusammengesetzten Funktionen: Z.B. f(x)=(x³-2)*e(x²-3)
UPDATE: Konkretisierung: Nullstellen, Extrem- und Wendestellen, Tangenten, Änderungsrate (aber keine Symmetrie oder Fernverhalten!)
• Integrale bilden können, wenn eine Stammfunktion gegeben ist.
• Fläche zwischen Funktionen
Hinweis: Die Klausur wird keinen hilfsmittelfreien Teil enthalten, d.h. der GTR ist immer erlaubt. Allerdings können Aufgabe der Art "Berechne .... so dass die Rechnung auch ohne GTR nachvollziehbar ist!" gestellt werden, so dass komplette Rechenwege aufzuschreiben sind.
Übungshinweise im Lösungsarchiv:
Exponentialgleichungen: Im Abschnitt 1.1.4 von
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_1_4_2
bis
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_1_4_14
Ableiten: Abschnitte 1.2.2 bis 1.2.4, also von
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_2_1
bis
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_4_3
Integration:
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_3_1_1
bis
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_3_1_5
 (ggf. Lösungsarchiv reloaden!)
(ggf. Lösungsarchiv reloaden!)Funktionsuntersuchungen
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_4_3_1
bis
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_4_3_7
 (ggf. Lösungsarchiv reloaden!)
(ggf. Lösungsarchiv reloaden!) Exponentialfunktionen finden:
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_5_2_1
bis
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_5_2_5
 (ggf. Lösungsarchiv reloaden!)
(ggf. Lösungsarchiv reloaden!) 17.05.2020
Lieber Mathekurs,Erstens: Wenn ich richtig informiert bin, schreiben wir am Dienstag, den 26.05.2020 unsere nächste Matheklausur. Die Themen der Klausur werde ich hier zeitnah hineinschreiben.
Zweitens: Als Vorbereitung und Aufgabe für unsere Stunde am Dienstag macht ihr bitte folgendes:
Schaut Euch (Aufgabe 1.4.1.12) aus meinem Lösungsarchiv an:
http://www.plusplanet.de/loesungsarchiv/index.html#anker1_4_1_12
Hier werden alle möglichen Dinge bei einer bestimmten ganzrationalen Funktion untersucht. Bitte wendet diese Aufgabenstellung auf eine neue Funktion an:
Aufgabe:
Richte dich nach dem obigen Beispiel und untersuche die Funktion
f(x) = x²·e(-2x + 4)
auf:
A) Nullstellen
B) Symmetrie
C) Fernverhalten
D) Extrempunkte
E) Wendepunkte
F) Bestimme die Gleichung der Tangente in P(1|f(1))
G) Bestimme die mittlere Änderungsrate der Funktion im Intervall von 1 bis 3, d.h. 1<x<3
10.05.2020
Lieber Mathekurs,wir sehen uns ja am Dienstag wieder. Bis dahin bearbeitet Ihr bitte auf S131 die Nr1 und Nr2. Die Lösungen dazu stehen zwar hinten im Buch, sind aber viel zu knapp. Ich möchte sichergehen, dass alle von Euch die Grundlagen noch einmal wiederholen. In der Stunde lasse ich ggf. manche von Euch an die Tafel, um die Aufgaben zu lösen.
03.05.2020
Die Hausaufgabe zum ersten Mai war etwas umfangreicher. Daher jetzt eine etwas weniger aufwändige Aufgabe:Folgende Aufgabe bitte bis zum 8. Mai. bearbeiten und mir schicken:
Gegeben: f(x) = x² · ex · x³
Leite auf folgende zwei Arten ab und zeige, dass die Ableitungen jeweils identisch sind:
1) Erst f vereinfachen: x² und x³ dürfen zusammengefasst werden. Dann muss man nur noch einmal die Produktregel anwenden
2) Doppelte Anwendung der Produktregel: Lies die Funktion so: f(x) = (x² · ex ) · x³ und leite in einer Nebenrechnung erst den Klammerterm (x² · ex ) ab. Dann kann man die Produktregel ein weiteres Mal anwenden.
Die Abgabe kann auf zwei Wegen erfolgen:
• Entweder Ihr schickt eine E-Mail an mich mit Euren Lösungen,
• oder ihr gebt die Lösungen über folgendes Rückmeldeformular ein:
(Hinweis: Als Mal-Zeichen kann ganz einfach das Sternchen * verwendet werden)
26.04.2020
Lieber Mathekurs,herzlichen Dank für Eure Lösungen.
Ich möchte im Buch noch kurz einen Schritt zurückgehen und nochmal etwas Bekanntes trainieren.
Hier ein Erklärvideo, wie man Aufgabe 5c per Hand löst (ich habe die Aufgabe leicht abgewandelt - die Aufgabe 5c im Buch ist einfacher als meine Version). Die Monotonietabelle und Krümmungstabelle im Video sind letztlich die jeweiligen hinreichenden Bedingungen - ich habe versäumt, das in der Niederschrift extra zu vermerken.
http://www.plusplanet.de/video/20200427_mq1.mp4
Aufgabe: S125 Nr 5 c,d,e
Abgabe: bis Freitag, den 1. Mai um 16:00 Uhr
Bitte beachtet, dass die Aufgaben ohne GTR gelöst werden sollen. (Natürlich könnt ihr den GTR zur Überprüfung neben dem Papier liegen haben, aber ihr solltet die Ergebnisse auch ohne GTR erzeugen können.) D.h. die Niederschrift wird entsprechend ausführlich, denn ich will den gesamten Rechenweg bei Euch sehen.
Die Abgabe kann auf zwei Wegen erfolgen:
• Entweder Ihr schickt eine E-Mail an mich mit Euren Lösungen,
• oder ihr gebt die Lösungen über folgendes Rückmeldeformular ein:
(Hinweis: Als Mal-Zeichen kann ganz einfach das Sternchen * verwendet werden)
19.04.2020
Weiter gehts!Zum Aufwärmen möchte ich nocheinmal eine bekannte Aufgabe von Euch rechnen lassen - nur mit anderen Zahlen.
Bitte schreibt mir eine Email mit den Ergebnissen bis zum Freitag, den 24. April.
Lies im Buch S127/128 (wirklich lesen! Dann klappts auch mit der Aufgabe!)
Aufgabe 1: Folgende Funktion f(x) gibt den Zuwachs eines Fantasiebaumes in Meter pro Jahr (zum Zeitpunkt x Jahre ab Keimung, d.h. x > 0) an.
f(x) = 0,04·(x + 10)·e(-0,04·x)a) Zeichne die Funktion im GTR, so dass Du eine Darstellung wie ganz oben auf S127 erhälst (Betrachtungsfenster mit V-Win korrekt wählen!).
b) Berechne per Hand und mit dem GTR: Wann wächst die Pflanze nicht? (siehe Tabelle unten auf S127)
c) Wann ist die Wachstumsgeschwindigkeit am größten?
d) Wann nimmt die Wachstumsgeschwindigkeit am schnellsten ab?
Eine Stammfunktion von f(x) ist gegeben durch:
f(x) = (-x - 35)·e(-0,04·x)e) Wie viel ist die Pflanze in den ersten sechs Jahren gewachsen?
Bitte schickt mir (zur Überprüfung) die Ergebnisse als eine reine Text-Mail in dieser Gestalt:
A1b: .....
A1c: Zum Zeitpunkt x= ____ Jahre.
A1d: Zum Zeitpunkt x= ____ Jahre.
A1e: ____ Meter.
Update am 27.04.2020: Lösungen dieser Aufgabe:
A1b) Die Wachstumsrate ist immer größer als null (für x>0), daher wächst die Pflanze immer (nach dem Modell)
A1c) Maximumsuche liefert: größtes Wachstum bei x=15 mit 0.5488 m/Jahr .
A1d) Minimumsuche der Ableitung liefert: x=39.999 (GTR) und rechnerisch: x=40. (der GTR rechnet hier leicht ungenau!)
A1e) Die Pflanze ist in den ersten 6 Jahren ca 2.74 m gewachsen.
Hinweise zur "per Hand"-Rechnung:
f'(x) = 0,04·(0.6-0.04·x)·e(-0,04·x)f''(x) = 0,04·(-0.064+0.0016·x)·e(-0,04·x)06.04.2020
Lieber Mathekurs,ich habe zwar noch nicht von allen die Lösungen erhalten, aber hier sind meine (Kurz-)Lösungen:
A1b: Die Pflanze wächst nach dem Modell immer, da es im Beobachtungszeitraum keine Nullstellen gibt.
A1c: nach 15 Jahren
A1e: 2,81 Meter gewachsen. (Integral von 0 bis 5 über f)
A2a:
c=19800
a= 9teWurzel(62100/19800) = 1.135425
A2b:
t= 9 62100 (Aufgabenstellung, 29.März)
t=10 70509 (30.März)
t=11 80058 (31.März)
t=12 90900 (1.April)
t=13 103210 (2.April)
t=14 117188 (3.April)
t=15 133058 (4.April)
t=16 151077 (5.April)
t=17 171537 (6.April)
t=18 194767 (7.April)
t=19 221144 (8.April)
t=20 251092 (9.April)
Die Johns-Hopkins-Universität meldet heute, am 6. April, eine Zahl von etwa 100000 Infizierten in Deutschland. D.h. unsere Prognose (171537) liegt jetzt schon schwer daneben.
Was bedeutet das? Und jetzt die Frage für die Oberchecker:
Wenn man bei https://coronavirus.jhu.edu/map.html erst Deutschland anwählt und dann unten rechts die Skalierung "Logarithmic" einstellt, so erhält man eine sich abflachende Kurve. Was bedeutet das im Zusammenhang mit unserer offenbar falschen Prognose?
Schöne Ferien und Gesundheit Euch allen!
30.03.2020
(Beachte zunächst den Eintrag vom 29.3!)Aufgaben bis Donnerstag, den 2. April
Lies im Buch S127/128 (wirklich lesen! Dann klappts auch mit der Aufgabe!)
Aufgabe 1: Folgende Funktion f(x) gibt den Zuwachs eines Fantasiebaumes in Meter pro Jahr (zum Zeitpunkt x Jahre ab Keimung, d.h. x > 0) an.

a) Zeichne die Funktion im GTR, so dass Du eine Darstellung wie ganz oben auf S127 erhälst (Betrachtungsfenster mit V-Win korrekt wählen!).
b) Berechne per Hand und mit dem GTR: Wann wächst die Pflanze nicht? (siehe Tabelle unten auf S127)
c) Wann ist die Wachstumsgeschwindigkeit am größten?
d) Wann nimmt die Wachstumsgeschwindigkeit am schnellsten ab?
Eine Stammfunktion von f(x) ist gegeben durch:
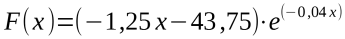
e) Wie viel ist die Pflanze in den ersten fünf Jahren gewachsen?
Aufgabe 2: (Wiederholung, ggf. S99ff noch einmal lesen)
Die Johns-Hopkins-Universität veröffentlicht tagesaktuell Zahlen zur Corona-Pandemie:
https://coronavirus.jhu.edu/map.html (Link für die Interessierten)
Dort lassen sich für Deutschland folgende Zahlen entnehmen:
Am 20.3. lag die Zahl der Infizierten bei ca. 19800 Personen.
Am 29.3. lag die Zahl der Infizierten bei ca. 62100 Personen.
Ihr sollt nun eine Prognose für die nächsten 10 Tage erstellen.
Wir gehen bei der Entwicklung von exponentiellem Wachstum aus, d.h. wir modellieren die Entwicklung mit einer Funktion der Gestalt:
i(t) = c · at ("i von t gleich c mal a hoch t")
Wir legen außerdem fest: t ist die Anzahl der Tage ab dem 20.3, d.h. t=2 entspricht dem 22.März und t=12 entspricht dem 1.April.
i(t) ist die Anzahl der Infizierten zum Tag t.
Wir wissen nun:
i(0) = 19800 und
i(9) = 62100
Wir haben also zwei Gleichungen, wo jeweils c und a unbestimmt sind.
a) Ermittle die Werte von c und a für unsere Prognosefunktion.
b) Berechne alle Funktionswerte für den ersten bis zum zehnten April.
Wir werden sehen, ob unsere Prognose eintrifft.
Bitte schickt mir (zur Überprüfung) bis Donnerstag, den 2. April eine reine Text-Mail mit folgenden Ergebnissen in dieser Gestalt:
A1c: nach ___ Jahren
A1e: ___ Meter gewachsen.
A2a: c= ___ / a= ____
A2b: i(2)=_____ i(3)=______ .....(etc.) i(11) = _____
29.03.2020
Lieber Mathe-GrundkursIch mache folgende Feststellung: Nur 15 von 25 Kursteilnehmern haben den Test absolviert (ich kann sehen, welche das sind - Ihr musstet ja Euren Namen eingeben). Bei diesen Leuten gehe ich davon aus, dass gewissenhaft gearbeitet wurde. Die restlichen 10 Leute schicken mir bitte die Hausaufgaben (der Abschnitt mit dem Datum 25.03) als Foto an

Eine weitere Hausaufgabe werde ich zeitnah hier veröffentlichen.
25.03.2020
Lieber Mathe GrundkursBis Sonntag, den 29. März bearbeitet ihr bitte folgende Aufgaben:
Aufgabe 1:
Bearbeitet S125 Nr5 a,b,c,f
Aufgabe 2:
Bearbeite diesen Test:
http://plusplanet.de/quizmeister_mq1_20200325/
Bitte nehmt Euch etwas Zeit, um Eure Fehler zu betrachten. Der Test ist nicht umfangreich (nur vier Fragen), aber auf der Ergebnisseite erscheint bei vielen Antwortmöglichkeiten eine Erklärung, aus der man lernen sollte.
22.03.2020
Auch bei Euch werde ich in den nächsten Tagen einen kleinen Test einstellen. Bitte nehmt die Aufgaben unten also ernst.Als neue Aufgabe bis Dienstag, den 24. März ist folgendes zu bearbeiten:
Seite 125 Nr 1 und Nr 2.
Bitte denke dabei an den Satz vom Nullprodukt, die pq-Formel und die Tatsache, dass "e hoch irgendwas" immer ungleich Null ist.
19.03.2020
Zunächst hier der Direktlink zur Hausaufgabe (im Lösungsarchiv):http://www.plusplanet.de/loesungsarchiv/index.html#anker1_4_3_4
Vor zwei Tagen hatte ich ja bereits empfohlen, dass ihr Euch im Lösungsarchiv umseht. Hier ein paar konkrete Übungen aus dem Lösungsarchiv (es sind heute noch zwei neue Aufgaben dazugekommen):
Aufgabe 1.2.2.1: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_2_1
Aufgabe 1.2.2.2: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_2_2
Aufgabe 1.2.2.3: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_2_3
Aufgabe 1.2.3.1: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_3_1
Aufgabe 1.2.3.2: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_3_2
Aufgabe 1.2.3.3: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_3_3
Aufgabe 1.2.4.1: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_4_1
Aufgabe 1.2.4.2: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_4_2
Aufgabe 1.2.4.3: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_2_4_3
Und noch eine Funktionsuntersuchung:
Aufgabe 1.4.3.1: http://www.plusplanet.de/loesungsarchiv/index.html#anker1_4_3_1
Bitte trainiert Euch mit diesen Übungen! Wer's nicht tut, hat später bei der Klausur einen schlechten Stand.
17.03.2020
Lieber Mathe-Kurs G4,In der kommenden Zeit möchte ich sicherstellen, dass die neuen Ableitungsregeln von Euch beherrscht werden.
Dazu könnt ihr in erster Linie mit den Aufgaben aus dem Lösungsarchiv arbeiten (siehe den Link links unten in der Seitennavigationsleiste). Hier sucht ihr bitte nach:
"Produktregel"
"Kettenregel"
"Verschiedene Regeln kombiniert"
Die Hausaufgabe werde ich später noch zum Lösungsarchiv hinzufügen.
.
Ich werde in einigen Tagen einen kleinen Online-Test darüber durchführen (Details dazu gibt's später).
07.01.2020
Lösungen der Nachprüfung:20200105_Loesungen_Test_Q1.jpg
Klausurthemen für die Klausur
* Wdh: Garantiert nochmal eine Aufgabe aus dem Test
* Produktsummen: Dies ist die Idee, die der Integralrechnung zugrunde liegt
* Integral und Stammfunktion: Definitionen, Hauptsatz, Berechnung per Hand und im GTR
* Integrale unterhalb der x-Achse
* Rechenregel für Integrale: Das Integral von f im Intervall [2;4] plus Integral von f im Intervall [4;5] ist gleich dem Integral von f im Intervall [2;5]
* Integrale im Sachzusammenhang
Beispiele dazu, die ich auch in der Klausur (angepasst) verwenden werde:
Verschiedene Integralaufgaben: 20200105_mq1_misc_integralaufgaben.jpg
Aufgabe zu Produktsummen: 20191128_produktsummen2.jpg
Lösungen zu den Aufgaben: 20200105_mq1_produktsummen_a.jpg und 20200105_mq1_produktsummen_b.jpg
Aufgabe im Sachzusammenhang: 20200105_Zapfsaeule_Loesung.jpg
Aufgaben aus dem Buch:
S 52 Nr4
S 62 Nr 10 und 11
S 65 Nr 6
17.12.2019
Zusammenhang Integralrechnung und Differentialrechnung20191216_Integral_u_Ableitung_Zusammenhang.jpg
10.12.2019
Klausurmusterlösung:20191111_MQ1G4_Klausur_Musterloesung_mit_allem8.pdf
28.11.2019
Produktsummen:20191128_produktsummen2.jpg
Fallunterscheidungen bei Funktionenscharen
f(x) = ax² + 1
Nullstellen:
f(x) = 0
ax² + 1 = 0 | -1
ax² = -1 |÷a
x² = -1/a | ±√
_______
x = +-√(-1/a)
Wurzel ist berechenbar, falls -1/a > 0
Dies gilt nur, falls a<0 ist!
Beispiel: a=-4, dann liegen die Nullstellen
_________ _____
bei: x = ±√(-1/(-4)) = ±√(1/4) = +-0,5
Übung: Berechne die Extrema von:
f(x) = ax² + x
f'(x) = 2ax + 1
f''(x)= 2a
Notwendige Bedingung für Extrema:
f'(x) = 0
2ax + 1 = 0 | -1
2ax = -1 | ÷2a für a ≠ 0
x = -1/(2a)
Sonderfall a=0: Dann ist f(x)=0·x² + x = x
Und diese Funktion ist eine lineare Funktion,
also eine Gerade (ohne Extrempunkte).
Hinreichende Bedingung für Extrema:
Wir wissen, dass f'(-1/(2a)) = 0 ist und
es gilt f''(-1/(2a)) = 2a ⎨ > 0 für a>0 -> TP
⎩ < 0 für a<0 -> HP
y-Wert: f(-1/(2a)) = a·(-1/(2a))² + (-1/(2a))
= a· 1/(4a²) - 1/(2a)
= 1/(4a) - 1/(2a)
= 1/(4a) - 2/(4a)
= -1/(4a)
08.11.2019
Kleiner Hinweis zu den Operatoren:
06.11.2019
Übungstipps für die Klausur:In meinem Lösungsarchiv (siehe drittletzter Eintrag in der Menüleiste links) gibt es einige relevante Aufgaben:
Abschnitt: Gleichungen
Unterabschnitt: Grundlagen Termumformungen (alles relevant)
Unterabschnitt: Lineare Gleichungen (alles relevant)
Unterabschnitt: Quadratische Gleichungen (alles relevant)
Abschnitt: Ableiten
Unterabschnitt: Ganzrationale Funktionen (alles relevant)
Abschnitt: Integrieren
Abschnitt: Funktionsuntersuchnungen
Unterabschnitt: Ganzrationale Funktionen (alles relevant)
Unterabschnitt: Funktionenscharen (ganzrational) (alles relevant)
Abschnitt: Steckbriefaufgaben
Unterabschnitt: Ganzrationale Funktionen (alles relevant)
05.11.2019
Themen für die Klausur am 12.11.2019- Grundlagen: Bruchrechnung, Potenzregeln
- Nullstellen von Funktionen bestimmen (x ausklammern, SvNP und quadratische Gleichungen beherrschen!!!)
- Ableitungen bilden können (Vorsicht: Funktion ggf. vorher in Standardform bringen!)
- Extrempunkte bestimmen mit anständiger Abhandlung der notwendigen und hinreichenden Bedingung
- Monotonietabelle erstellen und interpretieren können
- Fernverhalten bei ganzrationalen Funktionen
- Symmetrieuntersuchung (Achsensym. und Punktsym. - durch Betrachtung der Exponenten bei einer ganzrationalen Funktion in Standardform) und ggf. Ausnutzung von Symmetrie
- Wendepunkte bestimmen mit anständiger Abhandlung der notwendigen und hinreichenden Bedingung
- Extremwertprobleme ("Ziegenwiese" und Co.)
- Steckbriefaufgaben: Bedingungen aufstellen können und die dabei entstehenden LGS mit dem GTR lösen können
- Funktionenscharen: prinzipiell alle obigen Dinge auch bei Funktionen mit Parameter durchführen können.
- Umgang mit dem GTR: Funktionen zeichnen können (Achtung: Betrachtungsfenster einstellen können!) Funktionswerte mit der Trace-Funktion ablesen können, Nullstellen, Hoch- und Tiefpunkte bestimmen können.
21.10.2019
Material aus dem vergangenen Unterricht
http://www.plusplanet.de/miscrawhtml/ana_extremwertaufg_ziegenwiese.md.html
http://www.plusplanet.de/miscrawhtml/ana_steckbrief.md.html
http://www.plusplanet.de/miscrawhtml/ana_steckbrief2.md.html
27.09.2019
Beispiele für Extremwertaufgaben
http://www.plusplanet.de/miscrawhtml/20190920_mq1_ziegenwiese.md.html
10.09.2019
Ableitungen skizzieren und überprüfen lassen! Bewege die Kontrollpunkte der blauen Funktion so, dass sie die Ableitung der schwarzen Funktion darstellt!
* Mit Reset Graph kann ein neuer schwarzer Graph erzeugt werden
* Show Accuracy zeigt einen Wert für die Genauigkeit der Schätzung an. Wer über 90% kommt, hat den Zusammenhang gut verstanden
* Show Results zeigt die wirkliche Ableitungsfunktion in rot (nicht mogeln!)
http://webspace.ship.edu/msrenault/GeoGebraCalculus/derivative_try_to_graph.html